Why Common Core’s Math Standards Don’t Measure Up (by Guest Blogger Ze’ev Wurman)

Guest Post by Ze’ev Wurman (biography below) 

Last year William Schmidt and Richard Houang published a paper in the Educational Researcher that claimed to have explored the coherence of the Common Core state standards in mathematics (CCSSM) and their similarity to those of other high achieving nations. The study (Schmidt & Houang, “Curricular Coherence and the Common Core State Standards for Mathematics,” 41(8), 2012) has received significant attention, and defenders of the Common Core started to use it in support of their claims of CCSSM’s high quality. Schmidt himself testified before the Michigan House Education Committee last March and made the following claims.

• Common Core’s standards are very consistent with the standards in the world’s top-achieving countries;
• States with standards like the Common Core are the ones that did the best on the National Assessment of Educational Progress (NAEP);
• The Common Core is “coherent” and “hierarchical,” unlike many of the state standards it replaced.

The 2012 study Schmidt and Houang published does not support Schmidt’s claims. In their study Schmidt and Houang analyzed the CCSSM and coded them “applying the same methodology” used in their study of the A+ (high-achieving) countries that participated in the Third International Mathematics and Science Study (TIMSS) in 1995. However, the graduate students who did the actual coding in 2012 were clearly incompetent to perform this task.

[quote align=”left” color=”#999999″]Ze’ev Wurman on why the 2012 Schmidt and Houang Common Core paper does not show what its senior author claims it does.[/quote]

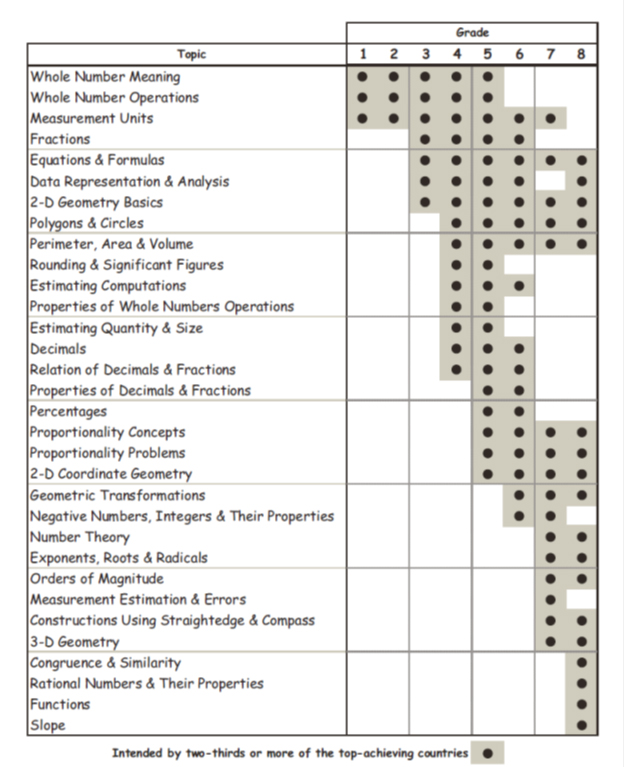
For example, Figure 2 in the paper (see below) shows “Constructions Using Straightedge & Compass” and “Systematic Counting” in the Common Core in grade 7. This is incorrect. The Common Core does not teach geometric constructions in grade 7. They are taught in the high school Geometry course (“Make formal geometric constructions with a variety of tools and methods (compass and straightedge, …”). The grade 7 standard that probably confused the authors’ graduate students is “Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions.” As another example, systematic counting, described by Schmidt himself in his 1997 book as dealing with permutation and combinations, is introduced by the Common Core in an advanced high school standard (“Use permutations and combinations to compute probabilities of compound events and solve problems”), not in the grade 7 standard (“Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation”), whose wording may have confused them. There are more examples of such sloppy miscoding of the Common Core, all of which fundamentally undermine any reliable conclusion one can draw from the authors’ analysis of the Common Core, despite the claim of applying the methodology used in the earlier study.

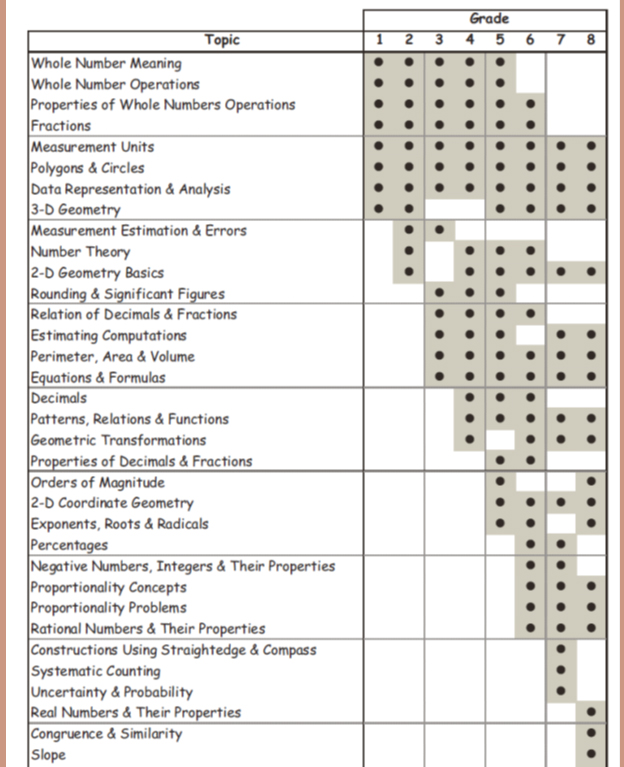
The problems with Figure 2 aren’t just with sloppy coding. Schmidt and Houang wanted to show that the results for the Common Core closely match those of the TIMSS A+ countries displayed in Figure 1. Unfortunately, they do not. But to make them appear similar, the authors rearranged the rows in Figure 2 so that the regular progression of topics over the years shown in Figure 1 appears to exist also in Figure 2. Indeed, Schmidt and Houang do not hesitate to argue that “Looking first at a visual representation, we note that Figure 2 representing the CCSSM bears a strong resemblance to Figure 1, at least in terms of its general shape.” But it does so only after they have reshuffled the rows in Figure 2 to create the illusion of a similar shape.

In fact, one can clearly see the falsity of this illusion in Figure 3, where the two are superimposed on each other. Suddenly the regular progression of mathematics topics in the TIMSS A+ countries displayed in Figure 1 (marked with dots) has completely disappeared. Nevertheless, Schmidt and Houang claim that those figures have “almost total congruence,” or “almost 85% degree of consistency with the CCSSM.” Yet if one simply counts the grids in Figure 3 (each grid box denoting a “topic-year”), CCSSM has 131 topic-years filled, with 45 of them not present in the A+ countries, while 15 of the topic-years of the A+ countries are not covered by CCSSM. In total, 60 out of 131 topic-years, almost half (46%) are misaligned between the TIMSS A+ countries and CCSSM, not the 15% Schmidt and Houang imply. So much for the claim that the Common Core is “very consistent” with the world’s top leading and achieving countries.

Nor does the 2012 Schmidt and Houang study show that states whose standards were more like CCSSM were more successful on the NAEP. First, they find to their chagrin that the old standards of California and Michigan, mediocre achievers on the NAEP, are much more aligned with CCSSM than those of Massachusetts or Vermont, top NAEP achievers (Table 2). Rather than accept the evidence on its face value, Schmidt and Houang decided to explore new ideas of alignment by adding other loosely-related measures to the usually-accepted alignment between CCSSM and state standards … until they found one that shows what they wanted it to show (Table 4). As a colleague quipped when I showed him their trick, “they torture the data until it confesses.”

In conclusion, Schmidt and Houang’s own data do not support the claim that the topic progression in the CCSSM are similar to the progressions of the TIMSS A+ countries, nor that states that did better on the NAEP had standards more closely aligned with the CCSSM. Further, their claim of “coherence” and “hierarchy” for the CCSSM is achieved only by reshuffling of CCSSM content coverage charts so they will seem to look like those of the successful nations.

Ze’ev Wurman was a U.S. Department of Education official under George W. Bush, is currently an executive with MonolithIC 3D Inc. In 2010 Wurman served on the California Academic Content Standards Commission that evaluated the suitability of Common Core’s standards for California, and is coauthor with Sandra Stotsky of “Common Core’s Standards Still Don’t Make the Grade” (Pioneer Institute, 2010).

Figures 1-3:

Figure 1: Mathematics topics intended at each grade by at least two thirds of the top-achieving countries (Original order of Topics)

Figure 2: Mathematics topics intended in the Common Core State Standards (Reshuffled order of Topics to make CCSS look like the Original)

Figure 3: Mathematics topics intended at each grade in top-achieving countries compared to the Common Core State Standards
(Note how the Original TIMSS orderly sequence, the dots, now has no rhyme or reason)